Geometride kullanılan açılarda açının yönü gözardı edilerek sadece ölçüsü dikkate alınır. Trigonometride kullanılan açılarda ise açının büyüklüğüne ek olarak yönü de önemlidir. Yönüne göre ölçüsü pozitif ya da negatif olabilen bu tip açılar yönlü açı olarak adlandırılır.
Bir yönlü açı saat yönünün tersi yönde ise ölçüsü pozitif, saat yönünde ise ölçüsü negatiftir.
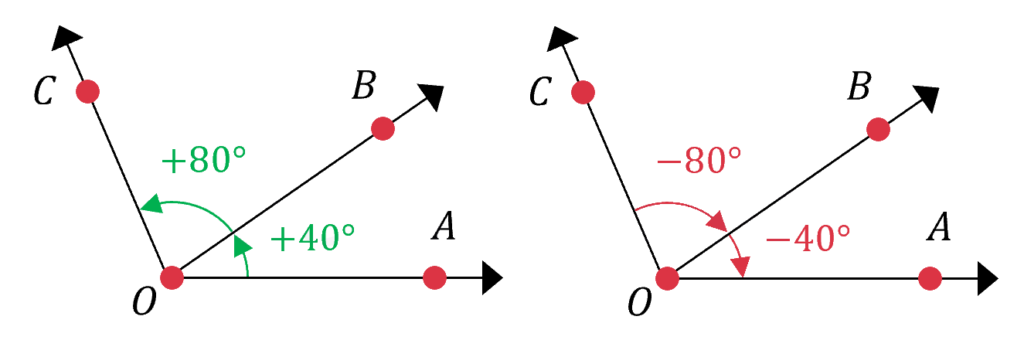
Pozitif ve negatif yönlü açılar
Açı Ölçü Birimleri
Belirli bir uzunluğu ölçmek için kilometre ve mil gibi farklı birimler kullanıldığı gibi, açıların ölçüleri için de farklı birimler kullanılır. Trigonometride en sık kullanılan iki açı ölçü birimi derece ve radyandır (bir diğer birim olan graddan burada bahsetmeyeceğiz).
Derece
Bir tam çember yayının 360 eş parçaya bölünmesiyle elde edilen yaylardan her birini gören merkez açının ölçüsüne 1 derece denir ve 1° ile gösterilir. Dörtte bir, yarım ve tam çember yaylarını gören merkez açılar sırasıyla 90°, 180° ve 360° olur.
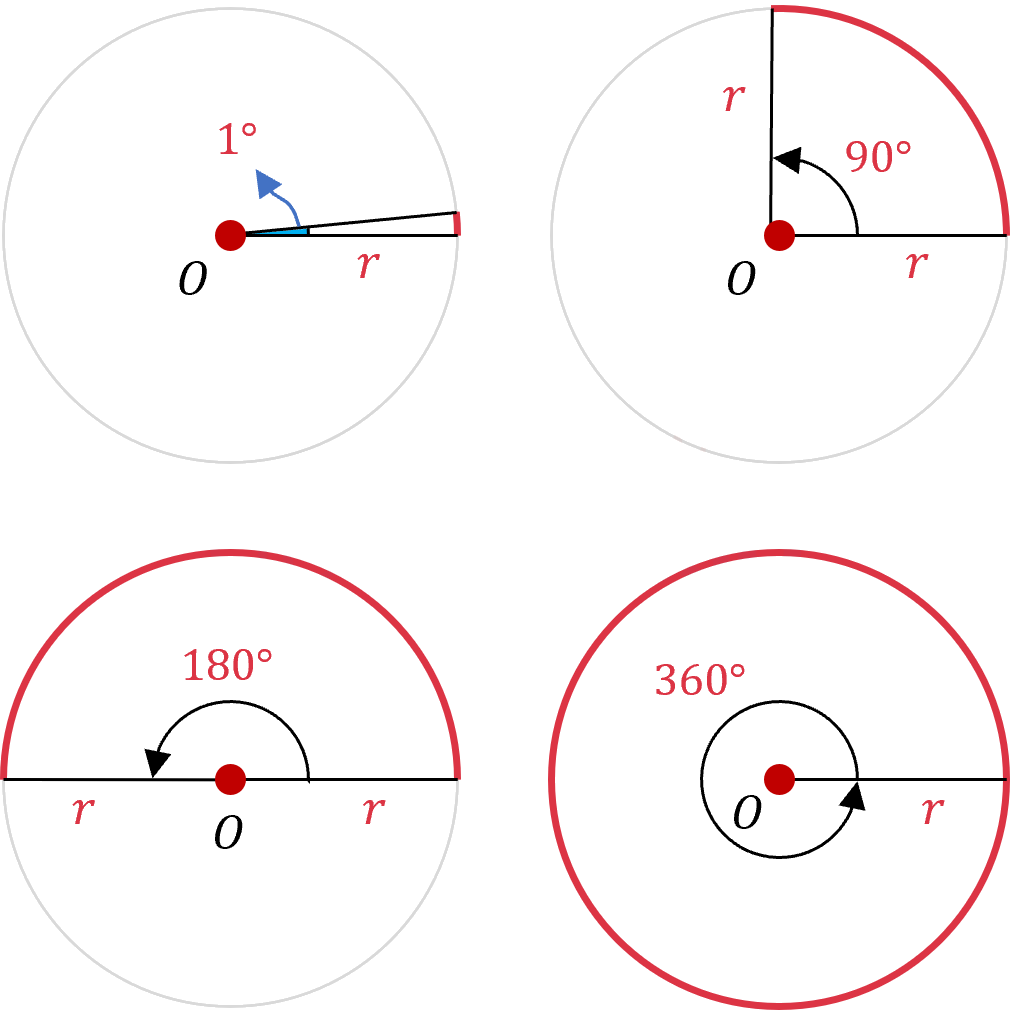
Derece cinsinden açılar
Bir dereceden daha küçük açıları ifade etmek için dakika ve saniye birimleri kullanılır. Bir derecenin 60'ta birine dakika denir ve (') sembolü ile gösterilir. Bir dakikanın 60'ta birine saniye denir ve ('') sembolü ile gösterilir. Bir açının ölçüsü a derece b dakika ve c saniye ise bu açı a° b' c'' biçiminde gösterilir.
1 derece=60 dakika=3600 saniye
1°=60′=3600″
1 tam çember yayı=360° =(360⋅60)′ =(360⋅60⋅60)″
ÖRNEK:
45,625 derecenin dakika ve saniye cinsinden yazılışı:
45,625°=45°+0,625°
=45°+0,625(60′)
=45°+37,5′
=45°+37′+0,5′
=45°+37′+0,5(60″)
=45°+37′+30″
45,625°=45° 37′ 30″
32° 18′ 45″ derecenin ondalık gösterimi:
=32+18/60+45/3600
=32+0,3+0,0125
=32,3125°
BİLGİ:
Bir tam çemberin 360'a bölündüğü derece sisteminin en yaygın kullanılan açı ölçü birimi olmasının bir sebebi 360'ın çok bölenli bir sayı olmasıdır. 360'ın 24 pozitif böleni vardır ve 1-10 arası sayılardan 7 hariç tümü 360'ın bir bölenidir, bu da kesirli sayılara girmeden bir tam çemberin farklı şekillerde bölünebilmesine imkan sağlar.
360 dışında akla gelebilecek bir diğer seçenek olan 100'ün ise sadece 9 pozitif böleni vardır.
İki pozitif açının ölçüleri toplamı 90° ise bu açılara tümler açılar denir. İki pozitif açının ölçüleri toplamı 180° ise bu açılara bütünler açılar denir.
Radyan
Bir çemberde yarıçap (r) uzunluğundaki bir yayı gören merkez açının ölçüsüne 1 radyan denir. Dörtte bir çemberin yay uzunluğu πr/2, yarım çemberin yay uzunluğu πr, tam çemberin yay uzunluğu 2πr olduğu için, bu yayları gören merkez açılar sırasıyla π/2, π ve 2π radyandır.
Bir dereceden daha küçük açıları ifade etmek için dakika ve saniye birimleri kullanılır. Bir derecenin 60'ta birine dakika denir ve (') sembolü ile gösterilir. Bir dakikanın 60'ta birine saniye denir ve ('') sembolü ile gösterilir. Bir açının ölçüsü a derece b dakika ve c saniye ise bu açı a° b' c'' biçiminde gösterilir.

Radyan cinsinden açılar
Yarıçap uzunluğunda yayı gören merkez açı radyan=1 radyan
Dörtte bir çemberi gören merkez açı radyan=π/2 radyan=90°
Yarım çemberi gören merkez açı radyan=π radyan=180°
Tam çemberi gören merkez açı =2π radyan=360°
ÖRNEK:
1 radyanın yaklaşık derece karşılığı:
2π radyan=360°
1 radyan= x°
x=360°/2π
π ≈ 3,14
x ≈ 57,29°
Derece-Radyan Arası Dönüşümler
Bir tam çember yayını gören merkez açı derece cinsinden ve radyan cinsinden olduğu için, iki birim arasındaki ilişki aşağıdaki şekilde kurulabilir.
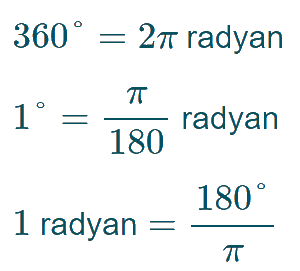
Buna göre derece cinsinden verilen bir açı ölçüsünü radyana çevirmek için açı
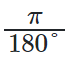
ile çarpılır.
ÖRNEK:
Radyan cinsinden verilen bir açı ölçüsünü dereceye çevirmek için açı
( \frac{180°}{\pi} )ile çarpılır. Alternatif olarak, açı ölçüsü π içeriyorsa π yerine 180° yazılarak da açı ölçüsü radyandan dereceye çevrilebilir.Esas Ölçü
Geometride açı ölçüleri 0° ile 360° aralığı ile sınırlanmıştır, ancak yönlü açılar için böyle bir sınırlama yoktur. Örneğin bir tekerleğin ya da CD'nin pek çok tur dönüşü sırasında katettiği toplam açı ölçüsü 360°'den büyük olmaktadır. Açı ölçüleri reel sayılar kümesinde herhangi bir değer alabiliyor olsa da, her açının bir tam çember üzerinde karşılık geldiği tek bir açı vardır ve işlemler çoğu zaman bu açı üzerinden yapılır.
Aşağıdaki şekildeki dereceleri 40°, 400° ve 760° olan üç açının gerçek ölçüleri farklı olsa da, 0-360° aralığında karşılık geldikleri açının ölçüsü aynıdır ve 40°'dir.
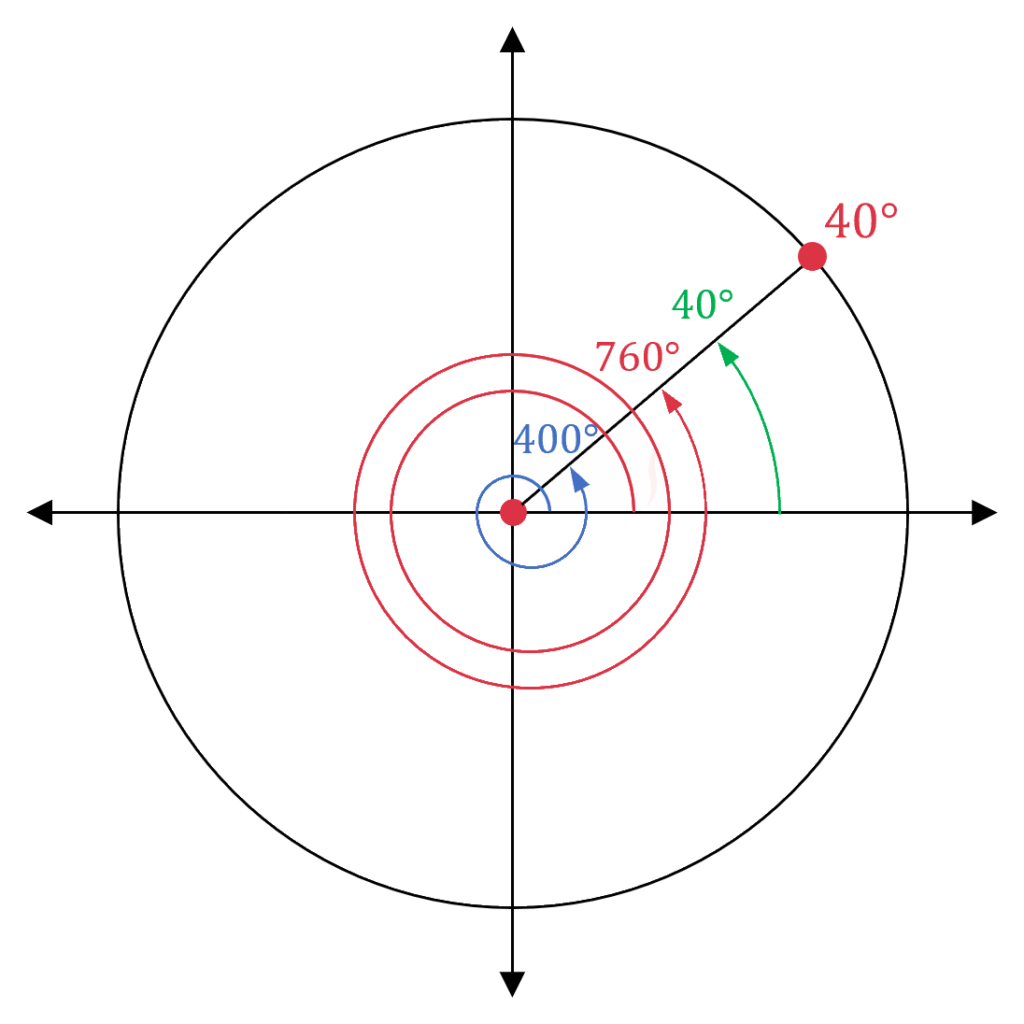
Gerçek açıları farklı, esas ölçüleri aynı üç açı
Bir açının içerdiği tam çember dönüşleri çıkarıldıktan sonra geriye kalan derece cinsinden ( [0°, 360°] ) ve radyan cinsinden ( [0, 2\pi] ) aralığındaki değere o açının esas ölçüsü denir. Bir açının gerçek ölçüsü negatif ise esas ölçü bu açıyı ( [0°, 360°] ) ya da ( [0, 2\pi] ) aralığına getirecek kadar tam çember dönüşü eklenerek elde edilir.
Derece Cinsinden Esas Ölçünün Bulunması
Bir açının derece birimindeki gerçek ve esas ölçüleri arasındaki ilişki aşağıda verilmiştir.
( 0° \le \alpha \lt 360° ) ve ( k\in\mathbb{Z} )
olmak üzere,
( \beta = \alpha + 360° \cdot k )
ise,
( \alpha ) değeri ( \beta )
gerçek açı ölçüsünün derece cinsinden esas ölçüsüdür.
Aşağıda gerçek ölçüleri verilen açıların tümünün esas ölçüsü ( 220° )'dir.
( \ldots = -500° = -140° = \textcolor{red}{220°} ) ( = 580° = \ldots )
( 580° = 220° + 360° \cdot 1 )
( -140° = 220° + 360° \cdot (-1) )
( -500° = 220° + 360° \cdot (-2) )
Ölçüsü derece biriminde verilmiş bir açının esas ölçüsünü bulmak için aşağıdaki yöntemler kullanılabilir.Gerçek açı ölçüsü pozitif ise bu değer 360°'ye bölünür. Bölme işleminin kalanı açının esas ölçüsüdür.
Buna göre gerçek ölçüsü ( 2000° ) olan açının esas ölçüsü ( 200° ) olur.
Gerçek açı ölçüsü negatif ise bu değeri pozitif yapan 360°'nin en küçük tam sayı katı açı ölçüsüne eklenir (360°, 720°, 1080°, ... ). Bu işlemin sonucu açının esas ölçüsüdür.