Trigonometri (Yunanca trigōnon "üçgen" + metron "ölçmek"), üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri, sinüs ve kosinüs gibi trigonometrik işlevlerin (fonksiyon) üzerine kurulmuştur ve günümüzde fizik ve mühendislik alanlarında sıkça kullanılmaktadır.
Tarihçe
Matematiğin doğrudan doğruya astronomiden çıkmış bir kolu olan trigonometrinin bazı ögeleri, daha Babilliler ve Eski Mısırlılar döneminde biliniyor, Sümerli astronomlar ilk kez bir çemberi 360 eşit parçaya bölerek açı ölçümünü yaptılar. Eski Yunanlar Menelaos’un küresel geometrisi aracılığıyla, bir daire içine çizilebilen dörtgenden yola çıkarak daire yaylarının kirişlerinin değerlerini veren çizgiler oluşturuyorlardı. Daha sonra Araplar, yay kirişlerinin yerine sinüsleri koyup; tanjant, kotanjant, sekant, kosekant kavramlarını geliştirdiler. İlk kez Akdeniz in çevresi trigonometre ile Abbasiler döneminde ölçülmüştür.

Batıda Nasîrüddin Tûsî’den büyük ölçüde yararlanan Regiomontanus’un üçgen üstüne adlı eseriyle gerçek trigonometri doğmuş oldu. François Viète ve Simon Stevin, hesaplarda ondalık sayılardan yararlandılar. John Napier logaritmayı işe kattı. Isaac Newton ve öğrencileri trigonometri işlevlerinin ve logaritmalarının hesabına tam serileri uyguladılar. Daha sonra da Leonhard Euler, birim olarak trigonometrik cetvelin yarıçapını alarak, modern trigonometrinin temellerini attı.
Genel bakış
Trigonometrik işlevler

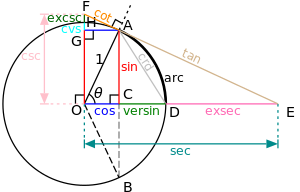
Trigonometrik işlevler bir dik üçgen ya da birim çember üzerinden tanımlanır. Temel olarak üç tane trigonometrik işlev ve bunların çarpma işlemine göre terslerinden oluşan üç tane daha işlev vardır. Yandaki ABC üçgeninde
- Sinüs işlevi (sin), karşı kenarın hipotenüse oranıdır.
- Kosinüs işlevi (cos), komşu kenarın hipotenüse oranıdır.
- Tanjant işlevi (tan), karşı kenarın komşu kenarı oranıdır.
Bir de bu işlevlerin çarpmaya göre tersi vardır. kosekant, sekant ve
Bu işlevler geometrinin dolayısıyla fiziğin ve mühendisliğin pek çok alanında kullanılır. Sinüs ve kosinüs teoremleri bir üçgenin açıları ve kenarlarını hesaplamakta kullanılır ki herhangi bir çokgen üçgenlerin birleşimi olduğundan çokgenleri incelemede de yararlıdır.
Birim çember ve esas ölçü
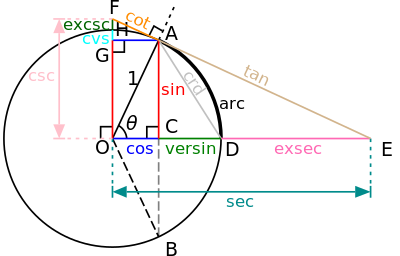
Yukarıda dik üçgen üzerinden yapılan tanım sadece 0-90 derece aralığını kapsar (0-π/2 radyan).
90-360 derece arasındaki açıların trigonometrik değerleri birim çember üzerinden hesaplanır. 360 dereceden büyük açılar 360 üzerinden devrettirilerek 0-360 arasındaki esas ölçüsü bulunur.
- 0° ≤x <360° ve k bir tam sayı olmak üzere ölçüsü (x + 360k) olan açıların esas ölçüsü x derecedir.
- 0 ≤ x< 2π ve k bir tam sayı olmak üzere, ölçüsü (x + 2πk) olan açıların esas ölçüsü x radyandır.
Merkezi orijin ve yarıçapı 1 birim olan çembere birim çember veya trigonometrik çember denir. Birim çemberin denklemi x2+y2=1 şeklindedir.
Sarma işlevi
Gerçel sayılar kümesinden birim çember üzerindeki noktalara tanımlanan işleve sarma işlevi denir.
Sarma işlevini s ile, birim çemberi de C ile gösterirsek işlev
şeklinde yazılabilir ve


olur. Başka bir deyişle, sarma işlevi, gerçel sayılar üzerinde dönemi (periyodu) 
İşlevler arasındaki ilişkiler
Yukarıdaki tanımlardan görülebileceği gibi, bu işlevler arasında
ilişkileri vardır.







 (
(
